There Is No Pure Empirical Reasoning

As the title says, there is no such thing as pure empirical reasoning.*

[ *Based on: “There Is No Pure Empirical Reasoning,” Philosophy and Phenomenological Research 95 (2017): 592-613. ]

1. The Issue

Empiricists think that all substantive knowledge about the world must be justified (directly or indirectly) by observation. This is taken to mean there is no synthetic, a priori knowledge.

By empirical reasoning, I mean a kind of (i) nondeductive reasoning (ii) from observations that (iii) provides adequate justification for its conclusion. The paradigms are induction and scientific reasoning in general.

Empirical reasoning is pure when it does not depend upon any synthetic, a priori inputs (i.e., a priori justification for any synthetic claim).

Empiricists would claim that all empirical reasoning is pure. I claim that no empirical reasoning is pure; empirical reasoning always depends on substantive a priori input. Empiricism is therefore untenable.

2. Empiricism Has No Coherent Account of Empirical Reasons

2.1. The Need for Background Probabilities

Say you have a hypothesis H and evidence E. Bayes’ Theorem tells us:

P(H|E) = P(H)*P(E|H) / [P(H)*P(E|H) + P(~H)*P(E|~H)]

To determine the probability of the hypothesis in the light of the evidence, you need to first know the prior probability of the hypothesis, P(H), plus the conditional probabilities, P(E|H) and P(E|~H). Note a few things about this:

1. This is substantive (non-analytic) information. There will in general (except in a measure-zero class of cases) be coherent probability distributions that assign any values between 0 and 1 to each of these probabilities.

2. This information is not observational. You cannot see a probability with your eyes.

3. These probabilities cannot, on pain of infinite regress, always be arrived at by empirical reasoning.

So you need substantive, non-empirical information in order to do empirical reasoning.

This argument doesn’t have any unreasonable assumptions. I’m not assuming that probability theory tells us everything about evidential support, nor that there are always perfectly precise probabilities for everything. I’m only assuming that, when a hypothesis is adequately justified by some evidence, there is an objective fact that that hypothesis isn’t improbable on that evidence.

Now for some examples:

BIVH

Compare two hypotheses about the origin of your sensory experiences:

RWH: You’re a normal person perceiving the real world.

BIVH: You’re a brain in a vat who is being fed a perfect simulation of the real world.

These theories predict exactly the same sensory experiences, so P(E|H) would be the same. Yet obviously you should believe RWH, not BIVH. This can only be because RWH has a higher prior probability. It can’t be that you learned that ~BIVH, or that P(BIVH) is low, empirically, since all your evidence is exactly the way it would be if BIVH were true. It must be that BIVH has a low a priori probability.

Precognition

In 2011, the psychologist Daryl Bem published a paper reporting evidence for a kind of precognition involving backwards causation. He had done nine experiments, in which eight showed statistically significant evidence for precognition.

When I first heard this, my reaction was skeptical, to say the least. I did not then accept precognition, nor did I even withhold judgement. Rather, I continued to disbelieve in precognition. I thought there must be something wrong with the experiments, or that the results had been obtained by luck. (This case illustrates the unreliability of currently accepted statistical methodology—but that is a story for another time.)

That is how rational people in general reacted. But we would not have reacted in that way to other results; e.g., if a study found that people tend to be happier on sunny days, we would have accepted the results at face value. This case illustrates that the rational reaction to some evidence depends upon the prior probability of the hypothesis that the evidence is said to support. Precognition is just so unlikely on its face that this evidence isn’t enough to justify believing in it.

Grue

You observe a lot of green emeralds. You then infer that it’s at least likely now that all emeralds are green. However, you do not infer that it’s at all likely that all emeralds are grue, even though that inference would be formally parallel.

[Definition: An object is grue iff (it is first observed before 2025 A.D. and it is green, or it is not observed before 2025 A.D. and it is blue).]

This case illustrates different conditional probabilities: the probability of unobserved emeralds being green, given that observed emeralds have been green, is higher than the probability of unobserved emeralds being grue given that observed emeralds have been grue.

This fact about conditional probabilities is, again, a priori, not empirical. This sort of thing can’t in general be learned by empirical reasoning, because you need this information in order to make any empirical inferences.

2.2. My Argument > Russell’s Argument

Bertrand Russell also defended rationalism by appealing to empirical reasoning. He said that to make inductive inferences, you have to know the correct rules of induction. That knowledge could not itself be arrived at by induction, on pain of circularity. It also can’t be gained by observation. So it must be a priori.

Against Russell’s argument, empiricists could say that you do not need to know the rules of inference in order to gain knowledge by reasoning; to think that you do is to confuse inference rules with premises. Rather, to gain inferential knowledge, you only need to know your premises, and then be disposed to follow the actually correct rules in reasoning from those premises.

Some empiricists have in fact said this, and this is the main response, as far as I know, to Russell’s argument. Some also claim that rule circularity (unlike premise circularity) is okay, so you can use inference to the best explanation in drawing the conclusion that inference to the best explanation is a good form of reasoning.

Well, you may or may not agree with that response. But in any case, my argument avoids it, which makes it better than Russell’s argument. My argument could not be accused of confusing inference rules with premises, because I am not saying that you need to have a priori knowledge about rules of inference. I am saying that you need to have a priori prior probabilities for hypotheses. This is really a lot more like having a priori knowledge of premises than it is like having a priori knowledge of rules of inference.

2.3. Skepticism Is Irrational

One could not plausibly respond by just rejecting empirical reasoning (as Hume did). First, because inductive skepticism is ridiculous. It’s ridiculous to deny that we have more reason to think that water is made of hydrogen and oxygen than we have to think that it’s made of uranium and chlorine.

Second, the success of modern science is perhaps the main thing that motivated empiricism in the first place. It would be irrational then to reject all scientific reasoning just so you can cling to empiricism.

3. Subjective Bayesianism Won’t Save You

Subjective Bayesians think that it’s rationally permissible to start with any coherent set of initial probabilities, and then just update your beliefs by conditionalizing on whatever evidence you get. (To conditionalize, when you receive evidence E, you have to set your new P(H) to what was previously your P(H|E).) On this view, people can have very different degrees of belief, given the same evidence, and yet all be perfectly rational.

Subjective Bayesians sometimes try to make this sound better by appealing to convergence theorems. These show, roughly, that as you get more evidence, the effect of differing prior probabilities tends to wash out. I.e., with enough evidence, people with different priors will still tend to converge on the correct beliefs.

The problem is that there is no amount of evidence that, on the subjective Bayesian view, would make all rational observers converge. No matter how much evidence you have for a theory at any given time, there are still prior probabilities that would result in someone continuing to reject the theory in the light of that evidence. So subjectivists cannot account for the fact that, e.g., it would be definitely irrational, given our current evidence, for someone to believe that the Earth rests on the back of a giant turtle.

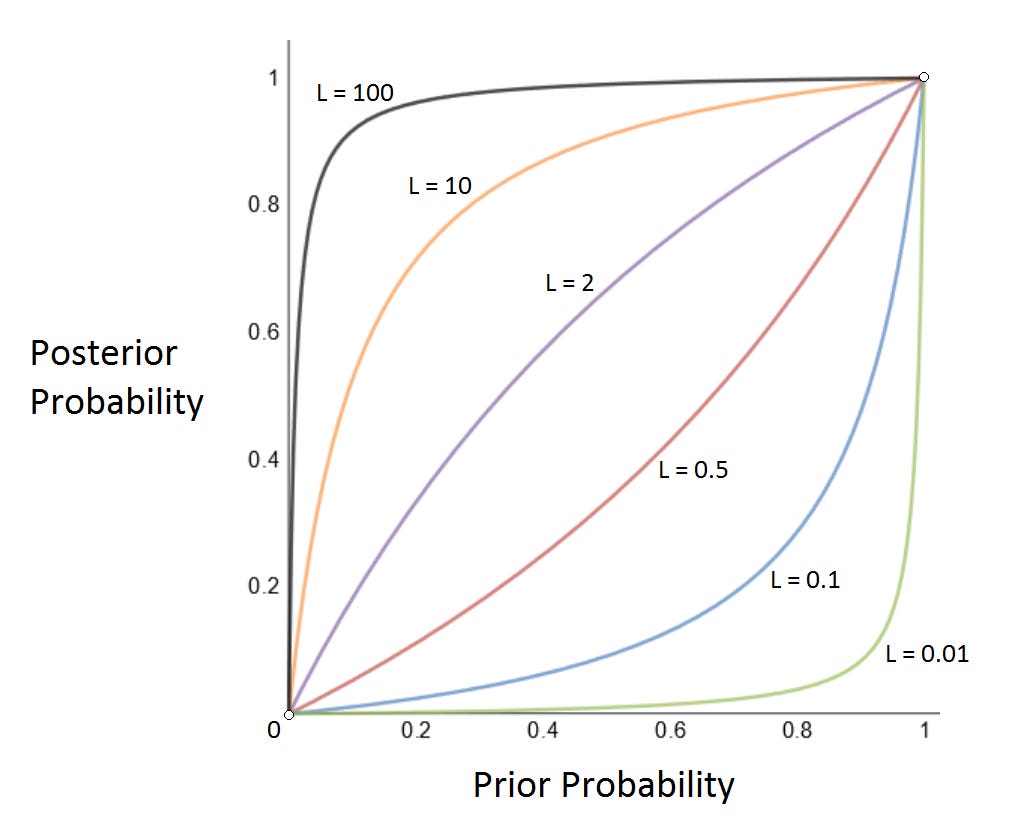
The point is illustrated by the following graph, which shows how the posterior probability of a hypothesis is related to its prior probability, for different values of the likelihood ratio, L.

Here, L is defined as P(E|H)/P(E|~H). (You can determine P(H|E) based on just two pieces of information, P(H) and L.) What you see in the graph is that the posterior probability is a (continuous, one-one) function of the prior probability. When L is greater than 1, then the curve is pulled upward, indicating that the posterior probability is greater than the prior, meaning that the hypothesis is supported. When L is <1, the curve is pulled downward, indicating disconfirmation.

But here is the important point: No matter what the value of L is, the graph is always a one-one function from the interval [0,1] onto the interval [0,1]. Thus, if the prior probability is completely unconstrained, then the posterior probability is also completely unconstrained. That is, if P(H) is allowed to be anything between 0 and 1, then P(H|E) can also be anything between 0 and 1.

Gathering more evidence doesn’t change this qualitative fact; gathering more evidence just gives you (typically) a more extreme likelihood ratio. But that still leaves you with the full range of possible posterior probabilities if you have the full range of possible priors going in.

Subjective Bayesians have no way of restricting the range of possible priors (that’s just their view). So they have no way of saying, for example, that it is an objective fact that we have good reason to think water is made of hydrogen and oxygen, or that it is objectively unreasonable, given our current evidence, to think that the Earth rests on the back of a giant turtle.

4. A Rationalist View

Rationalists believe that we have some a priori justification for some substantive (non-analytic) claims. In particular, we have a priori prior probabilities, which enable us to make empirical inferences.

The biggest problem with this view: How do we assign those prior probabilities? In many cases, it just is not at all obvious what they are. E.g., what is the a priori prior probability that water would be composed of hydrogen and oxygen? Or that life would have evolved by natural selection? No one knows how to answer that.

I’m not going to answer that here, either. But I’ll say one thing to make you feel better about not knowing the a priori prior probabilities of things: We don’t need to have perfectly precise a priori probabilities for every proposition. Rather, it’s enough if we can just say that there is a limited range (less than the full range from 0 to 1) of prior probabilities for a hypothesis that are rational. E.g., to do empirical reasoning about the Theory of Evolution, I don’t have to know exactly what the prior probability of Evolution is. I might just be able to say that its prior probability is more than 1 in a trillion, and less than 90%.

How could this be enough? Because in general, if you start with a restricted range of prior probabilities, then as you gather evidence, the range of allowable posterior probabilities in light of that evidence shrinks. The more evidence you collect, the narrower it gets. This is why, even though I have very little idea what the prior probability of the Theory of Evolution was, I have a good idea that its current probability, on my evidence, is well over 90%.

I have another diagram that illustrates the idea:

Suppose that I just know that the prior probability of a hypothesis is between 0.1 and 0.9. But then I collect a lot of evidence for it, so I build up a likelihood ration of 100. In that case, the posterior probability, P(H|E), is constrained to be between 0.917 and 0.999.

In general, if you get enough evidence, then you have a good idea what the posterior probability is, even if you had almost no idea what the prior was.