Non-Egalitarianism

Here, I prove that equality has no intrinsic value.*

[*Based on: “Non-Egalitarianism,” Philosophical Studies 114 (2003): 147-71.]

1. The Thesis

Egalitarianism holds that equality is intrinsically good, or (perhaps better) that inequality is intrinsically bad. I.e., it is intrinsically worse if people’s welfare levels are more unequal. Qualification: assume that we’re talking about people who are equally deserving, so you don’t raise issues about desert.

Note that we’re not talking about whether equality produces good or bad effects. We’re talking about whether it’s a good in itself. So it’s irrelevant to talk about how inequality might create incentives to be productive, how it might undermine freedom, etc.

Non-egalitarianism holds that equality is intrinsically neutral (neither good nor bad). We’re going to prove non-egalitarianism.

2. Some Principles

I think these principles are plausible:

A. Equality or inequality within a given individual’s life doesn’t matter. E.g., it doesn’t matter if the older you is better off than the younger you.

B. Supervenience: If two events are qualitatively identical, then they have the same intrinsic value.

C. Additivity: If you have events A and B occurring at different times, the value of the combined event (A&B) equals the value of A plus the value of B.

D. Transitivity: If A is equally good as B, and B is equally good as C, then A is equally good as C.

3. Three Possible Worlds

Consider three possible worlds:

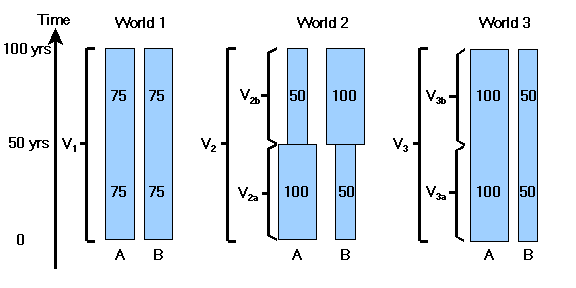
In all three worlds, there are two people, A and B, who are equally deserving and each live for 100 years. In World 1, each has a welfare level of 75 throughout their lives.

In World 2, person A is at a welfare level of 100 for the first half of his life, then at 50 for the second half. Person B has the reverse situation: first 50, then 100.

In World 3, person A has welfare 100 throughout his life, and B has welfare 50 throughout his life.

Let V1 be the value of world 1, V2 the value of world 2, and V3 the value of world 3. V2a is the value of the first half of world 2 and V2b the value of the second half. V3a is the value of the first half of world 3 and V3b the value of the second half.

4. The Proof

Here’s the argument:

1. V1=V2.

   • Explanation: each person has the same total welfare in both worlds (150); it is just distributed differently between the first and second halves of their lives. By principle (A) above, inequality within a given person’s life doesn’t matter.

2. V2a = V2b.

   • From the Supervenience principle (B) above. There’s no reason for either half of world 2 to be better than the other, so they must be equal.

3. V3a = V3b.

   • Ditto.

4. V2a = V3a.

   • Ditto. The first half of world 2 is identical to the first half of world 3.

5. V2 = V2a + V2b.

   • From the Additivity principle (C) above.

6. V3 = V3a + V3b.

   • From Additivity.

7. V2 = V3.

   • From 2-6 above. We have V2b = V2a = V3a = V3b. So V2a+V2b = V3a+V3b.

8. V1 = V3.

   • From 1, 7, by Transitivity (principle D above).

The conclusion is incompatible with egalitarianism. Worlds 1 and 3 have the same total utility, but world 1 is much more equal. If the two worlds are equally good, then it must be that equality doesn’t matter.

5. Esoteric Objection: Against Additivity

There is one objection that has prima facie force. It is that the Additivity principle begs the question and may be false.

Inequality obviously does not add over time, as shown by world 2: there is inequality at any given time in world 2, yet overall world 2 is perfectly egalitarian (A and B have the same overall total utility). Since inequality isn’t additive, obviously, if inequality affects value then value should not be additive over time. Because this connection is fairly obvious, you might think it begs the question to assume additivity over time.

Aside: That’s hardly a knock-down objection on its face. Given principles A, B, and D above, Egalitarianism entails ~Additivity, and Additivity entails ~Egalitarianism. The relationship is symmetrical. It’s no more “circular” on its face to use Additivity to justify rejecting Egalitarianism than it is to use Egalitarianism to justify rejecting Additivity. The rational approach would be to decide which of the two principles is intuitively more plausible. If you find Additivity more plausible, that’s a good reason to reject Egalitarianism.

Be that as it may, there is a further argument for Additivity. It is that you can get decision-theoretic paradoxes if you reject additivity over time.

Imagine World 4, which is just like World 3, except that you add a small benefit to B in the second half of his life (say, another 10 units of welfare). Stipulate that it’s not enough to make up for the disvalue of the inequality in the world, according to the Egalitarian view. Let V4b be the value of the second half of World 4.

On the egalitarian view, V2 > V4 since the added utility in World 4 doesn’t make up for the inequality. Also, obviously V4b > V3b since the only difference between World 4 and World 3 is a little more utility in the second half of World 4. V3b = V2b for reasons stated earlier (and note that this didn’t assume Additivity). So V4b > V2b.

So here’s the decision puzzle. Consider two choices:

Choice I: You’re informed that the first half of the world will be as in World 2 (which is the same as the first half of World 4). You’re then asked to choose whether the second half of the world should be 2b or 4b. You choose 4b, because we just said that V4b > V2b.

Choice II: You’re asked to choose whether the world as a whole should be like World 2 or World 4. In this case, you choose World 2, because we just said that V2 > V4.

This looks inconsistent. The two choice situations are really the same, yet different results seem rational depending on how you describe it. The best account of what went wrong is that it was a mistake to posit a violation of Additivity. I.e., it cannot really be true that V4b > V2b, yet V2 > V4.

6. Thoughts

So equality has no intrinsic value. This doesn’t show whether it has instrumental value. But it is interesting because many philosophers are intuitively inclined to think that inequality is intrinsically bad.

I also like to cite this as an example of how it is possible to have non-trivial proofs in ethics. There are not many ethical proofs, but there are a few.

Of course, most philosophers won’t accept the argument, because most philosophers are basically completely dogmatic and only use argumentation as a tool for rationalizing their prejudices. What they’re likely to do is reject one of the principles in section 2, based on the assumed truth of egalitarianism. (Notice how dogmatic that is—that’s a way that you could hold on to any position in the face of any argument.)