Does Probability Theory Refute Coherentism?

Here, I explain how probability theory doesn’t refute the Coherence Theory of Justification.*

[ *Based on: “Does Probability Theory Refute Coherentism?”, Journal of Philosophy 108 (2011): 35-54. ]

Caveat: This is a bit technical.

Aside: This paper holds my record for the longest review time: four and a half years (including one revision and resubmission).

1. Background

1.1. The Coherence Theory

The Coherence Theory of Justification (“Coherentism”) is meant as an alternative to foundationalism. Coherentists thus hold two key theses:

1. Non-foundationalism: No belief has any degree of foundational justification (i.e., justification independent of support by other beliefs).

2. Coherence Justification: Some beliefs are justified by coherence (i.e., mutual support relations among the beliefs, or something like that).

Example: you separately interview two witnesses to a crime. If they tell stories that independently agree with each other (without having conferred with each other), that’s evidence that their stories are true. Allegedly, this holds even if you would not have credited either witness’ testimony by itself.

This is supposed to be like how our belief-forming methods in general have no independent credibility, and yet when they converge on a coherent belief system, that belief system is justified.

1.2. My Earlier Criticism

I previously wrote an objection to coherentism, arguing that, in the witness scenario above, if each witness really has no independent credibility, then the combination of 2 witnesses’ testimony also has no credibility: https://fakenous.substack.com/p/probability-coherence-justification

I made this case using a simple model of the witness scenario. It apparently shows that the Coherentist’s view rests on a misunderstanding of probability theory. But note that this criticism required a third assumption:

3. Conditional Independence: The two witnesses’ testimonies are probabilistically independent of each other, conditional on the truth-value of the proposition they attest to. I.e., once you fix whether A is true or not, one witness’ asserting A does not affect the probability of the other witness asserting A.

This was my interpretation of the coherentist’s saying that the two witnesses “independently” converge on the same story.

In probability-theory terms, I interpreted the above three conditions as follows: Let

A = some proposition that we’re asking two witnesses about

W1 = [The first witness says that A]

W2 = [The second witness says that A]

Then we have:

1. Non-foundationalism: P(A|W1) = P(A|W2) = P(A)

2. Coherence Justification: P(A|W1,W2) > P(A)

3. Conditional Independence: P(W2|W1,A) = P(W2|A), and P(W2|W1,~A) = P(W2|~A)

I’m not going to go through the math in detail (either here or in the next subsection) because it’s tedious and you’d probably stop reading. But if you trust me on how the math works out, we can focus on what assumptions can be called into question.

So, (1)-(3) above are incompatible; there is no coherent probability distribution (satisfying the axioms of probability theory) that makes all of them true. I took that to refute the coherence theory.

1.3. The Truth-Conduciveness Objection to Coherentism

Later, other authors raised another problem. This problem assumes that the coherentist is committed to the view that coherence always adds justification to a set of beliefs. That is:

4. Truth-conduciveness: If two belief sets differ in their coherence, and other things are equal, then the more coherent belief set is more likely correct (i.e., the conjunction of all the beliefs has a higher probability).

The objection then holds that there is no way of measuring degree of coherence (subject to a few plausible other constraints) such that Truth-conduciveness comes out true. Again, it just conflicts with probability theory.

2. Avoiding my Earlier Objection

2.1. Rejecting Conditional Independence

As noted, my own objection to Coherentism relied on Conditional Independence:

P(W2|W1,A) = P(W2|A), and

P(W2|W1,~A) = P(W2|~A).

What I later realized was that the Coherentist need not accept that. The purpose of the independence condition was to avoid cases where witness #2 just asks witness #1 what he’s going to say, then deliberately says the same thing—in that sort of case, of course the coherence of the two testimonies does not enhance their credibility.

The Conditional Independence condition rules out that sort of case. But it’s also possible to rule out that sort of case using a weaker condition, such as:

P(W2|W1,~A) <= P(W2|~A)

That’s the condition that, if A is false, witness 1’s asserting it doesn’t make witness 2 more likely to assert it.

In general, the following condition is necessary and sufficient for the coherentist’s purposes:

P(W2|W1,A) > P(W2|W1,~A)

This is the condition that, given that the first witness asserts A, the other witness is more likely to concur if A is true than if A is false. There are coherent probability distributions that make that true along with Non-foundationalism. All such probability distributions make Coherence Justification true. So probability theory allows you to embrace Coherentism.

2.2. New Objection: Negative Coherence Justification

But now a new problem arises. We have the following three assumptions for the Coherentist:

1. P(A|W1) = P(A|W2) = P(A)

2. P(A|W1,W2) > P(A)

3. P(W2|W1,A) > P(W2|W1,~A)

It can be shown that these entail the following undesired conclusion:

Negative Coherence Justification: P(A|~W1,~W2) > P(A)

This says that if two witnesses “agree” in not asserting A, then that fact alone is evidence for A. I assume coherentists would not want that.

2.3. Solution

I see one reasonable way for coherentists to avoid this undesirable consequence. This is to question the interpretation of Non-foundationalism. We interpreted it as

P(A|W1) = P(A|W2) = P(A)

which says that if witness 1 asserts A, that doesn’t change the probability of A, and if witness 2 asserts A, that also doesn’t change the probability of A. That was an interpretation of the idea that a single source’s testimony by itself doesn’t have any credibility. But here’s a better interpretation of that idea:

P(A|W1,~W2) = P(A|W2,~W1) = P(A)

This says that if witness 1 asserts A and witness 2 doesn’t (so witness 2 either denies A or remains silent), that fails to change the probability of A; also, if witness 2 asserts A while witness 1 doesn’t, that fails to change the probability of A. On reflection, that’s a more accurate rendition of the claim that a single witness’ testimony by itself fails to provide justification for A.

So we can rewrite the Coherentist’s commitments like this:

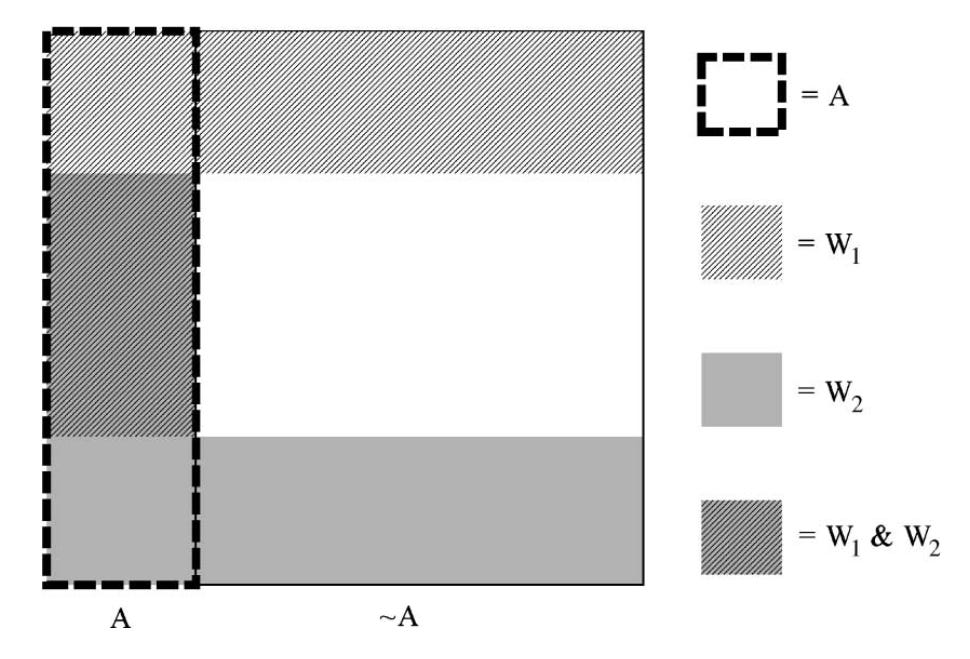
1. P(A|W1,~W2) = P(A|W2,~W1) = P(A)

2. P(A|W1,W2) > P(A)

3. P(W2|W1,A) > P(W2|W1,~A)

All of those are compatible, and they don’t entail negative coherence justification. I include a diagram from the paper showing a probability distribution that makes all of those true.

3. Avoiding the Truth-Conduciveness Objection

3.1. Assumptions

The Truth-Conduciveness Objection to Coherentism uses the following assumptions:

1. Conditional Independence, as described earlier.

2. Content-Determination: The coherence of a series of beliefs or witness reports is purely a function of the contents of those beliefs/reports. It doesn’t depend on any other features of the witnesses or how they made their reports, etc.

3. An interpretation of the “other things being equal” clause: Other things are equal between two series of witness reports as long as

   1. the reliabilities of the witnesses are the same (roughly, the initial probability of the nth witness in the first series of reports being correct equals the initial probability of the nth witness in the second series of reports being correct); and

   2. the prior probability of the contents of all the witness reports being correct is the same for the two series of reports. (One version of the theorem dispenses with (b).)

Given those assumptions, it can be proven that coherence does not always enhance probability of truth, even when other things are held equal. (I.e., on any measure of coherence, there must be cases in which coherence has no effect or actually lowers the probability of truth.)

But, should we accept those assumptions? We already rejected Conditional Independence above. I find the other two assumptions questionable as well.

3.2. Rejecting Content-Determination

The Coherentist can reasonably reject (2), Content-Determination. Consider two sets of witness reports:

Case 1: A witness asserts A. Then a second witness independently asserts A.

Case 2: A single witness asserts A twice.

If we’re trying to stay true to the Coherentist’s underlying intuition, Case 1 but not Case 2 is supposed to be an example of coherence justification. (You don’t get more justification merely by repeating yourself!)

So either the Coherentist doesn’t think that Coherence always produces justification, or the Coherentist thinks that Case 1 but not Case 2 is an example of coherence. But the contents of the two series of reports are the same in Case 1 and Case 2.

So the Coherentist should reject either the claim that Coherence always enhances justification, or the Content-Determination claim. Either way, the Truth-Conduciveness Argument shouldn’t phase them.

3.3. Re-interpreting “Other Things Being Equal”

The Truth-Conduciveness Objection to Coherentism claims that there is no possible measure of degree of coherence such that, when other things are held equal, increased coherence always results in increased likelihood of truth. This theorem crucially depends on the interpretation of the clause “other things are held equal”. As noted above, the proofs are going to need something like this:

3. Other things are equal provided

   1. the reliabilities of the witnesses are the same, and

   2. the prior probability of the contents of all the witness reports being correct is the same for the two series of reports.

Note that that gives a sufficient condition for other things to be equal. So here’s an objection: That condition isn’t sufficient, because here’s something else that has to happen for all other things to be equal:

c. The prior probability of each asserted proposition in the first series of reports must equal the prior probability for the corresponding proposition in the second series.

So, suppose that you have one series of witness reports, <A1, A2, … , An>, and another series of reports, <B1, B2, … , Bn>. Condition (b) above says that P(A1 & A2 & … & An) = P(B1 & B2 & … & Bn). But condition (c) imposes the stronger requirement that P(A1) = P(B1), P(A2) = P(B2), … , and P(An) = P(Bn).

Why accept (c)? Well, the prior probability of, say, the first report is presumably not itself determined by coherence. So it is an example of an “other thing” (a thing other than degree of coherence). So it should be held equal in order for “all other things” to be equal. Similarly for the prior probability of the second report, etc.

If you incorporate condition (c), then you can no longer prove the theorem used in the Truth-Conduciveness Objection.

4. Conclusion

Probability theory alone doesn’t refute Coherentism, after all. I still don’t think Coherentism is plausible, though.